A sequence got by starting with any number and adding a fixed number repeatedly is called an arithmetic sequence.
Example: 4, 7,10, 13, …….
1, 1½, 2, 2½, ……
13, 7, 1, -5, …….
Ans:
i) Sequence 1, 3, 5, 7, ……
It is an arithmetic sequence
Common difference, d = 3 – 1 =2
ii) Sequence 2, 4, 6, 8, ……
It is an arithmetic sequence
Common difference, d = 4 – 2 =2
Ans:
Sequence of
number of coloured squares : 8, 12, 16, 20, …..
It is an arithmetic sequence.
There is a common difference between
two consecutive terms.
Ans:
i) Sequence of
number of small squares: 2, 4, 6, 8, ......
ii) Sequence of
number of large squares: 0, 1, 2, 3, …..
iii) Sequence of
total number of squares: 2, 5, 8, 11, …..
All the above sequences are
arithmetic sequences.
Ans:
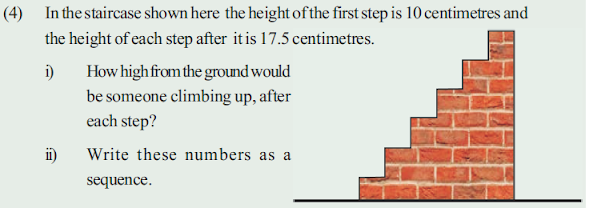
i) Height to
first step = 10cm
Height to 2nd step =
10+17.5 = 27.5cm
Height to 3rd step =
27.5+17.5 = 45cm
Height to 4th step = 45+17.5 = 62.5cm
ii) Sequence of heights of steps from the ground : 10, 27.5, 45, 62.5, 80, …..
3) The 5th
term of an arithmetic sequence is 38 and
the 9th term is 66. What is its 25th term?
Ans:
5th term = 38
9th term = 66
4) Is 101 a term of the arithmetic sequence 13, 24, 35, ….. ? What about 1001?
Ans:
d = 24 – 13 = 11
101 – 13 = 88
88
÷ 11 = 8
Since 88 is divisible by 11, 101
is a term of this sequence.
1001
– 13 = 988
988 is not divisible by 11
∴1001 𝑖𝑠 𝑛𝑜𝑡 𝑎 𝑡𝑒𝑟𝑚 𝑜𝑓 𝑡ℎ𝑖𝑠 𝑠𝑒𝑞𝑢𝑒𝑛𝑐e
5) How many three digit numbers are there, which leave a remainder 3 on division by 7?
Ans:
The least three digit number
which leaves a remainder 3 on division by 7 = 101
The largest three digit number
which leaves a remainder 3 on division by 7 = 997
d
= 7
101
+ 7(n – 1) = 997
7(n
– 1) = 997 – 101
7(n
– 1)= 896
n
– 1 = 896 ÷ 7 = 128
n
= 128 + 1
= 129
Ans:
The
algebraic form of any arithmetic sequence is of the form
Xn = an + b
Where a and b are
fixed numbers
Conversely, any sequence of this form is an arithmetic sequence.
nth term of an
arithmetic sequence
nth term of an arithmetic sequence, Xn = dn + (f – d)
n – number of terms,
d
– common difference
f – first term
Look at the following bird
problem.
One bird said, “We and we again
together with half of us and half of that, and one more is a natural number”.
Write all the possible number of
birds starting from the least. For each of these, write the sum told by the
bird also?
Find the algebraic expression of
these two sequences?
Sequence of number of birds : 4,
8, 12, …..
Xn = dn + (f – d) = 4n + (4 – 4) = 4n
Algebraic expression of the first sequence = 4n
Sequence of total number of birds
: 12, 23, 34, 45, …..
Xn = dn + (f – d) = 11n + (12 – 11)
= 11n + 1
Algebraic expression of the
second sequence = 11n + 1
For n = 5, Xn = 1
For n = 11, Xn = 2
For n = 17, Xn = 3
ie, the sequence contains all the natural numbers.
From the algebraic expression it
is clear that numerator is an odd number. An odd number divided by an odd
number will always be an odd number.
For n = 2, Xn = 1
For n = 5, Xn = 3
For n = 8, Xn = 5
ie, the sequence contains all the odd numbers but no even numbers.
Prove that
the squares of all the terms of the arithmetic sequence 4, 7, 10, …. belong to
the sequence.
Ans:
Sequence of squares of 4, 7, 10,
…. are 16, 49, 100,...
Xn
= dn + (f – d) = 3n + (4 – 3) = 3n
+ 1
Algebraic form of the sequence 4,
7, 10, …. is 3n + 1
The squares 16, 49, 100, … can be
expressed in the form of 3n + 1 for a natural number n.
∴ the squares
of all the terms of the arithmetic sequence 4, 7, 10, …. belong to the
sequence.
Prove that the arithmetic sequence 5, 8, 11, … contains no perfect squares.
Ans:
Xn = dn + (f – d) = 3n + ( 5 – 3) = 3n + 2
No perfect square can be
expressed in the form 3n + 2. for any natural number n.
Ans:
X11 + X14 = f + 10d + f
+ 13d
= 2f + 23d
X5
+ X20 = f + 4d + f + 19d
=2f + 23d
X11 + X14 = X5 + X20
The first
term of an arithmetic sequence is one and the sum of the first 4 terms is 100.
Find the first four terms?
Ans:
X1 +X2 + X3
+X4 = 100
X2 + X3 +X4
= 100 – X1 = 100 – 1 = 99
X3 = 99/3 = 33
X3 = X1 + 2d
1 + 2d = 33
2d = 32
d = 16
First four terms of the sequence
: 1, 17, 33, 49
Prove that
for any four consecutive terms of an arithmetic sequence, the sum of the two
terms on the two ends and the sum of the two terms in the middle are the same.
Ans:
X1 + X4 = f + f + 3d =
2f +3d
X2 + X3 = f + d +f +2d = 2f + 3d
∴ X1 + X4 = X2 + X3
Write four
arithmetic sequences with 100 as the sum of first four terms?
Ans:
Let first term = 10
X2 + X3 +X4
= 100 – 10 = 90
X3 = 90/3 = 30
X1 + 2d = 30
2d = 30 – 10 = 20
d = 10
Sequence : 10, 20, 30, 40, …
Let first term = 19
X2 + X3 +X4
= 100 – 19 = 81
X3 = 81/3 = 27
X1 + 2d = 27
2d = 27 – 19 = 8
d = 4
Sequence : 19, 23, 27, 31, …
Let first term = -20
X2 + X3 +X4
= 100 – (-20) = 100 + 20 = 120
X3 = 120/3 = 40
X1 + 2d = 40
2d = 40 – (-20) = 60
d = 30
Sequence : -20, 10, 40, 70, …
Let first term = 4
X2 + X3 +X4
= 100 – 4 = 96
X3 = 96/3 = 32
X1 + 2d = 32
2d = 32 – 4 = 28
d = 14
Sequence : 4, 18, 32, 46, …
i) X1
= 30
X1 +X2 + X3
= 300
X2 = 300/3 = 100
d = 100 – 30 = 70
First three terms of the sequence = 30,
100, 170
ii) First term =
30
X2 + X3 +X4
= 300 – 30 = 270
X3 = 270/3 = 90
X1 + 2d = 90
2d = 90 – 30 = 60
d = 30
First three terms of the sequence : 30, 60, 90
iii) X1
= 30
X1 +X2 + X3
+ X4 + X5 = 300
X3 = 300/5 = 60
X1 + 2d = 60
2d = 60 – 30 = 30
d = 15
First three terms of the sequence = 30, 45,
60
iv) X1
= 30
X1 +X2 + X3
+ X4 + X5 + X6 = 300
X2 + X3 +X4
+ X5 + X6 = 300 – 30 = 270
X4 = 270/5 = 54
X1 + 3d = 54
3d = 54 – 30 = 24
d = 8
First three terms of the sequence = 30, 38,
46
6
Ans:
i)Third term
is the middle term of the first five terms
∴third term= sum of 5 terms / 5
=
150/5 = 30
ii) Sum of five
terms from the sixth term = 550 – 150
= 400
Eighth term is the middle term of
five terms from 6th term
∴eighth term= sum of 5 terms from 6th term /5
= 400/5 = 80
iii) X3
= 30
X8 = 80
X3 + 5d = 80
30 + 5d = 80
5d = 80 – 30 = 50
d = 10
X1 + 2d = 30
X1 = 30 – 2d
= 30 – 20 = 10
First three terms are : 10, 20, 30
The angles
of a pentagon are in arithmetic sequence. Prove that its smallest angle is
greater than 360 .
Ans:
Sum of the angles of a pentagon =
(n – 2)180
= (5 – 2)180
= 3 ×180 = 540
Since the angles are in arithmetic sequence,
the third angle = 540/5=1080
Let the smallest angle be 360
X1 = 36
X3 = X1 +
2d
= 36 + 2d = 1080
2d = 108 – 36 = 72
d = 72/2=36
X5 = X1 +
4d
= 36 + 4×36
= 36 + 144 = 1800
An angle of a polygon should be
less than 1800 . The least angle should be
greater than 360
Write four
arithmetic sequences with 100 as the sum of first four terms?
Sequences : 22, 24, 26, 28
1, 17, 33, 49
16, 22, 28, 34
4, 18, 32, 46
Sum of first n consecutive natural numbers is half the product of the last
number and the next natural number.
Sum of first n consecutive natural numbers = 𝒏(𝒏+𝟏)/𝟐
Sum of the first n terms of an arithmetic sequence
What is the
difference between the sum of the first 20 terms and next 20 terms of the
arithmetic sequence 6, 10, 14, …?
Ans:
Sequence 1(starting from first
term) : 6, 10, 14,…
21st term of the
sequence = dn + (f – d)
=
4 × 21 + (6 – 4)
=
84 + 2 = 86
2nd sequence starting
from 21st term : 86, 90, 94, …
Difference of the corresponding
terms of the sequences
= 86 – 6 = 80
= 90 – 10 = 80 and so on
∴𝑑𝑖𝑓𝑓𝑒𝑟𝑒𝑛𝑐𝑒
𝑜𝑓 𝑡ℎ𝑒 𝑠𝑢𝑚𝑠 𝑜𝑓 𝑓𝑖𝑟𝑠𝑡
20 𝑡𝑒𝑟𝑚𝑠 𝑎𝑛𝑑 𝑛𝑒𝑥𝑡
20 𝑡𝑒𝑟𝑚𝑠
OR
Ans:
Sum of first 40 terms of the
sequence = (n/2)[2f +
(n – 1)d]
= 1/2×40[2×6 + (40 – 1)4]
= 20(12 +
39×4)
= 20 × 168 = 3360
Sum of first 20 terms of the
sequence = (n/2)[2f +
(n – 1)d]
= 1/2×20[2×6 + (20 – 1)4]
= 10(12 +
19×4)
= 10 × 88 = 880
Sum of 20 terms from 21st
term = 3360 – 880 = 2480
Difference of the sums of first
20 terms and next 20 terms of the sequence = 2480 – 880 = 1600
Calculate
the difference between the sums of the first 20 terms of the arithmetic
sequences 6, 10, 14, … and 15, 19, 23, …?
Ans:
Common difference of both the
sequences is 4
Difference between the
corresponding terms of the sequences = 15 – 6 = 9
= 19 – 10 = 9 and so on
∴ the
difference between the sums of the first 20 terms of the arithmetic sequences
6, 10, 14, … and 15, 19, 23,… = 20 ×9 = 180
OR
Ans:
Sum of first 20 terms of the
sequence 6, 10, 14,…
= (n/2)[2f +
(n – 1)d]
= 1/2×20[2×6 + (20 – 1)4]
= 10(12 +
19×4)
= 10 × 88 = 880
Sum of first 20 terms of the
sequence 15, 19, 23,…
= (n/2)[2f +
(n – 1)d]
= 1/2×20 [2×15 + (20 – 1)4]
= 10(30 + 19×4)
= 10 × 106 = 1060
Difference between the sums = 1060 – 880 = 180
Find the sum
of all three digit numbers which are multiples of 9?
Ans:
First term = 108
Last term = 999
d = 9
Xn
= dn + (f – d)
999 = 9n + (108 – 9)
9n + 99 = 999
9n = 999 – 99 = 900
n = 900/9 = 100
Sum of the terms = (n/2)(X1 + Xn)
= 1/2×100 (108 + 999)
=
50 × 1107
=
55350
Ans:
i) Sum of n terms = n2
+ 2n
first term = 12 + 2 ×1
= 1 + 2 = 3
sum of first two terms = 22 + 2 ×2
= 4 + 4 = 8
second term = 8 – 3 = 5
d = 5 – 3 = 2
Xn
= dn + (f – d)
= 2n + (3 – 2)
= 2n + 1
ii) Sum of n terms = 2n2
+ n
first term = 2 × 12 + 1
= 2 + 1 = 3
sum of first two terms = 2 × 22 + 2
= 8 + 2 = 10
second term = 10 – 3 = 7
d = 7 – 3 = 4
Xn
= dn + (f – d)
= 4n + (3 – 4)
= 4n – 1
iii) Sum of n terms = n2
− 2n
first term = 12 − 2 ×1
= 1 − 2 = -1
sum of first two terms = 22 − 2 ×2
= 4 − 4 = 0
second term = 0 – (-1) = 0 + 1 = 1
d = 1 – (-1) = 2
Xn
= dn + (f – d)
= 2n + (-1 – 2)
= 2n – 3
iv) Sum of n terms = 2n2
− n
first term = 2 × 12 − 1
= 2 − 1 = 1
sum of first two terms = 2 × 22 − 2
= 8 − 2 = 6
second term = 6 – 1 = 5
d = 5 – 1 = 4
Xn
= dn + (f – d)
= 4n + (1 – 4)
= 4n – 3
v) Sum of n terms = n2
− n
first term = 12 − 1
= 1 − 1 = 0
sum of first two terms = 22 − 2
= 4 − 2 = 2
second term = 2– 0 = 2
d = 2 – 0 = 2
Xn
= dn + (f – d)
= 2n + (0 – 2)
= 2n – 2
Ans:
i) 51 + 52 + 53 + …..+ 70
n = 20
sum = 20/2×(51 + 70)
=
10 × 121
=
1210
ii) 1½ + 2 ½ +3 ½ + …….+ 12 ½
n = 12
sum = 12/2×(1½ + 12½ )
=
6× 14
=
84
iii) ½ + 1 + 1½ + 2 + 2 ½ + ……. +
12 ½
n = 25
sum = 25/2×( 1/2 + 12 ½ )
= 25/2×13
= 325/2
= 162½
Ans:
Xn
= dn + (f – d)
= 8n + (16 – 8)
= 8n +8
Sum of n terms = a/2×𝒏 (𝒏+𝟏) + bn
=
8× n(𝒏+𝟏)/2 + 8n
=
4× n(n+1) + 8n
=4n2 + 4n + 8n = 4n2
+ 12n
When 9 is added the expression
becomes 4n2 + 12n + 9
4n2 + 12n + 9 = (2n)2
+ 2 ×2𝑛×3 + 32
= (2n + 3)2
It is a perfect square.
Ans:
i) Next two
lines of the pattern are: 11, 12, 13, 14, 15
16, 17, 18, 19, 20, 21
ii)Sequence of last terms of each
line : 1, 3, 6, 10, …
1 = 1
3= 1+2
6 = 1+2+3 and so on
∴𝑡ℎ𝑒 𝑙𝑎𝑠𝑡 𝑡𝑒𝑟𝑚
𝑜𝑓 𝑡ℎ𝑒 9𝑡ℎ 𝑙𝑖𝑛𝑒=1+2+3+
….+9
=
9×(9+1)/2 = 9 × 5 = 45
1st term in the tenth
line = 46
Last term in the tenth line = 45 + 10 = 55
iii) Sum of all the numbers in
the first ten lines = sum of natural
numbers from 1 to 55
= 55×(55+1)/2 = 55×56/2
=
55 × 28
=
1540
Ans:
Next two lines of the pattern
are: 34, 37, 40, 43, 46
49, 52, 55, 58, 61, 64
Sequence of last terms: 4, 10, 19, 31,…
4 = 1 + 3×1
10 = 1 + 3×3
19 = 1 + 3×6
31 = 1 + 3×10
1 = 1
3= 1+2
6 = 1+2+3 and so on
∴𝑠𝑢𝑚 𝑜𝑓 𝑓𝑖𝑟𝑠𝑡
19 𝑛𝑎𝑡𝑢𝑟𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟𝑠=1+2+3+
….+19
= 19×(19+1)/2 = 19 × 10 = 190
Last term of the 19th
line = 1 + 3 ×190
=
1 + 570 = 571
First term of 20th
line = 571 + 3 = 574
Last term of the 20th
line = 574 + 19 × 3
=
574 + 57 = 631



























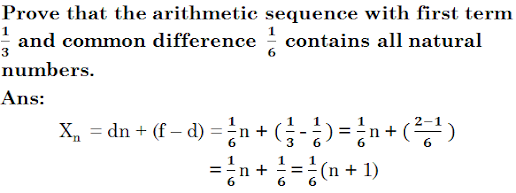






















.jpg)
.png)
.jpg)


.jpg)




0 Comments